Transformation

Jon Reades

What is it?

Data transformation just means changing the raw data in some way to make it more tractable for analysis.

For example:

  • Centering the mean on zero is an obvious example.
  • But we can also do quite complicated things (with caution!) in order to get a distribution that we can work with using statistical tests that have certain expectations about the data we’re feeding them.

Transformation in 1D

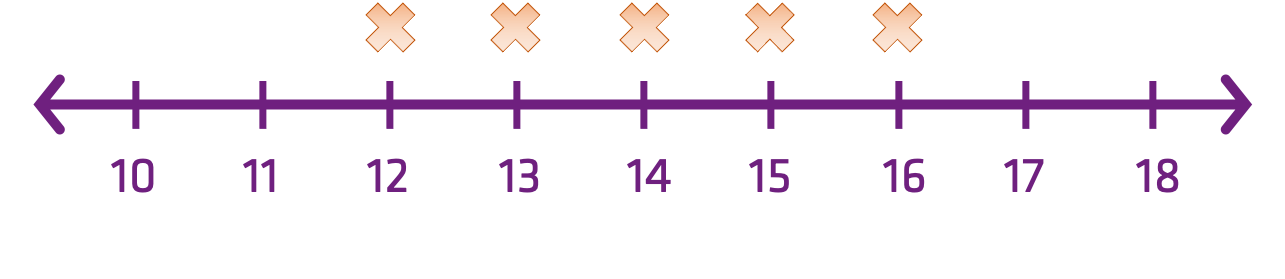
\[ x-\bar{x} \]

Input Output
12 -2
13 -1
14 0
15 +1
16 +2

So…

Transformations are mathematical operations applied to every observation in a data set that preserve some of the relationships between them.

For Example

If we subtract the mean from everyone’s height then we can immediately tell if someone is taller or shorter than we would expect.

If we subtract the mean from everyone’s income then we cannot immediately tell if someone is earning more or less that we would expect.

So what is a useful transformation in one context, may not be in another!

Fleshing This Out

Question: How can you tell if you did better than everyone else on the Quiz or on the Final Report?

Answer: Just subtracting the mean is not enough because the distributions are not the same. For that we also need to standardise the data in some way.

\[ z = \dfrac{x-\bar{x}}{\sigma} \]

Divide through by the distribution!

Standardisation

Z-Score Standardisation

\[ \dfrac{x-\bar{x}}{\sigma} \]

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(x)
print(scaler.mean_)
scaler.transform(x)

Interquartile Standardisation

\[ \dfrac{x_{i}-x_{Q2}}{x_{Q3}-x_{Q1}} \]

from sklearn.preprocessing import RobustScaler
trf = RobustScaler(
        quantile_range=(25.0,75.0)).fit(x)
trf.transform(x)

Interdecile Standardisation

\[ \dfrac{x_{i}-x_{50^{th}}}{x_{90^{th}}-x_{10^{th}}} \]

print("You've got this...")

What is the danger of not standardising by age when looking at long-term illness?

Group Standardisation

\[ x'_{a,i} = \dfrac{x_{ai}}{\sum_{g} r_{N,g} P_{a,g}} \]

Details:

  • \(x_{a,i}\) = Value of attribute i in area a.
  • \(P_{a,g}\) = Population of group g in area a.
  • \(r_{N,g}\) = National ratio N of group g
  • \(\sum\) = Sum for all groups.
  • \(x'_{a,i}\) = Standardised value of i in area a.

Normalisation

Proportional Normalisation

\[ \dfrac{x_{i}}{\sum{x}_{i=1}^{n}} \]

import numpy as np
x/np.sum(x)

Range Normalisation

\[ \dfrac{x_{i}-x_{min}}{x_{max}-x_{min}} \]

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(x)
print(scaler.data_max_)
scaler.transform(x)

Non-Linear Transformations

Log Transformation

Recall: logs are the inverse of exponentiation!

  • So if \(10^{3} = 1,000\) then \(log_{10}(1,000) = 3\).
  • And if \(10^{0} = 1\) then \(log_{10}(1) = 0\)
import numpy as np
xhat = np.log(x)

Why Log Transform?

Let’s assume that \(x = \{10, 100, 1000, 10000\}\), consider what happens if:

  • The formula for the mean is \(\frac{\sum{x}}{n}\).
  • The formula for variance is \(\frac{(x-\bar{x})^{2}}{n}\).

The Natural Log (\(e\)) has certain advantages over other logs and should probably be your default choice for log transformations.

Other Transforms…

  • Quantile (maps the PDF of each feature to a uniform distribution)
  • Square Root (often with count data)
  • Arcsine/Angular (with percentages, proportions, text)
  • Rank (with care on extreme distributions)
  • Box-Cox and Yeo-Johnson (arbitrary power transformations)

When Transforms Don’t Help

Arbitrarily transforming data isn’t a panacea. ‘Robust’ tests can be another approach when all else fails and two common approaches are:

  • Trimming: cutting off, say, the top and bottom 5% of scores would start to remove skew and offer a more useful view of the central tendency of the data.
  • Bootstrapping: taking many sub-samples (usually of \(n-1\) data points or similar) we can build a picture of how certain metrics vary.

One Last Note

The term normalization is used in many contexts, with distinct, but related, meanings. Basically, normalizing means transforming so as to render normal. When data are seen as vectors, normalizing means transforming the vector so that it has unit norm. When data are though of as random variables, normalizing means transforming to normal distribution. When the data are hypothesized to be normal, normalizing means transforming to unit variance.

Source: Stack Exchange

Transforming Spatial Data

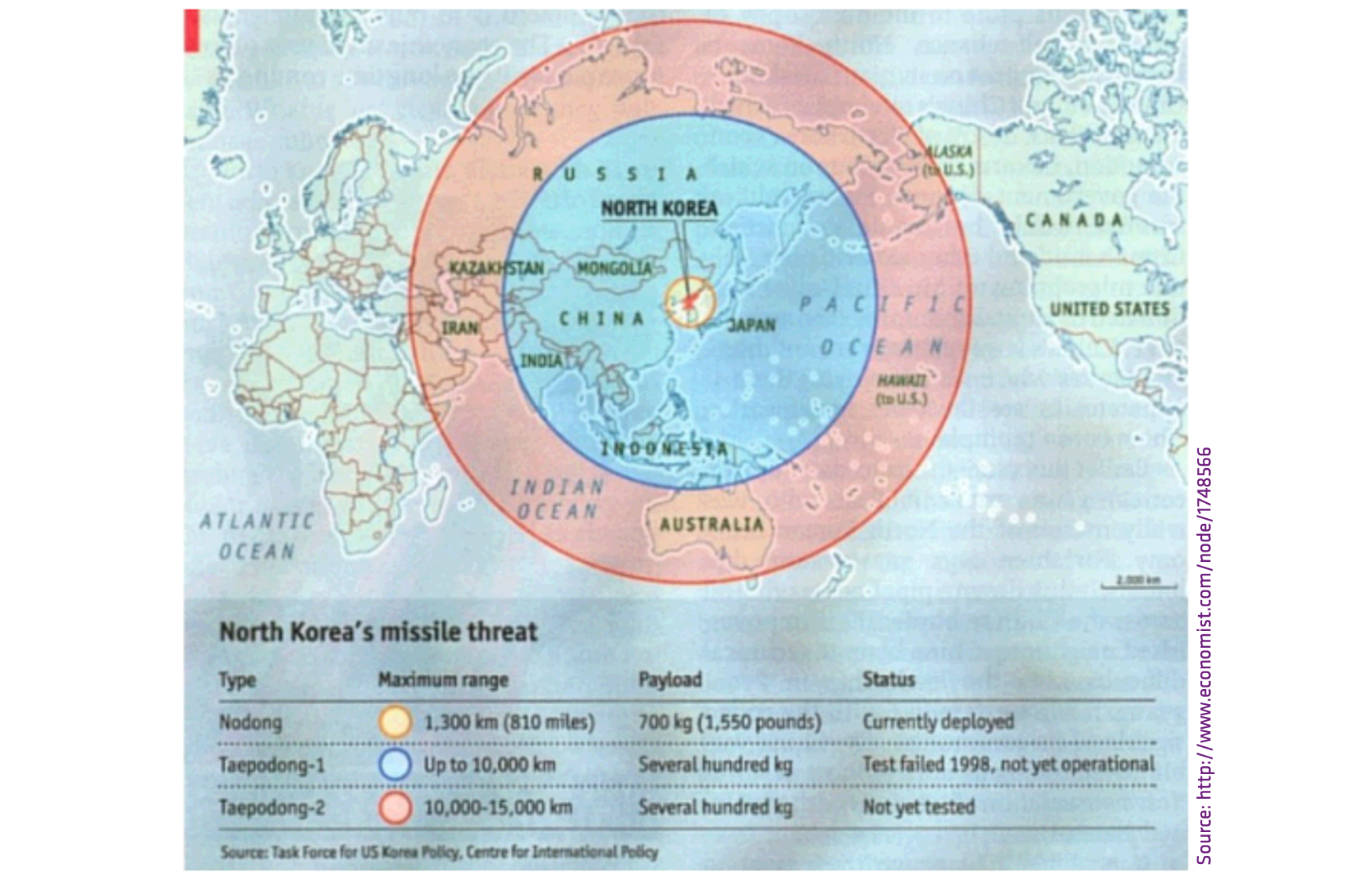
What’s Wrong with this Map?

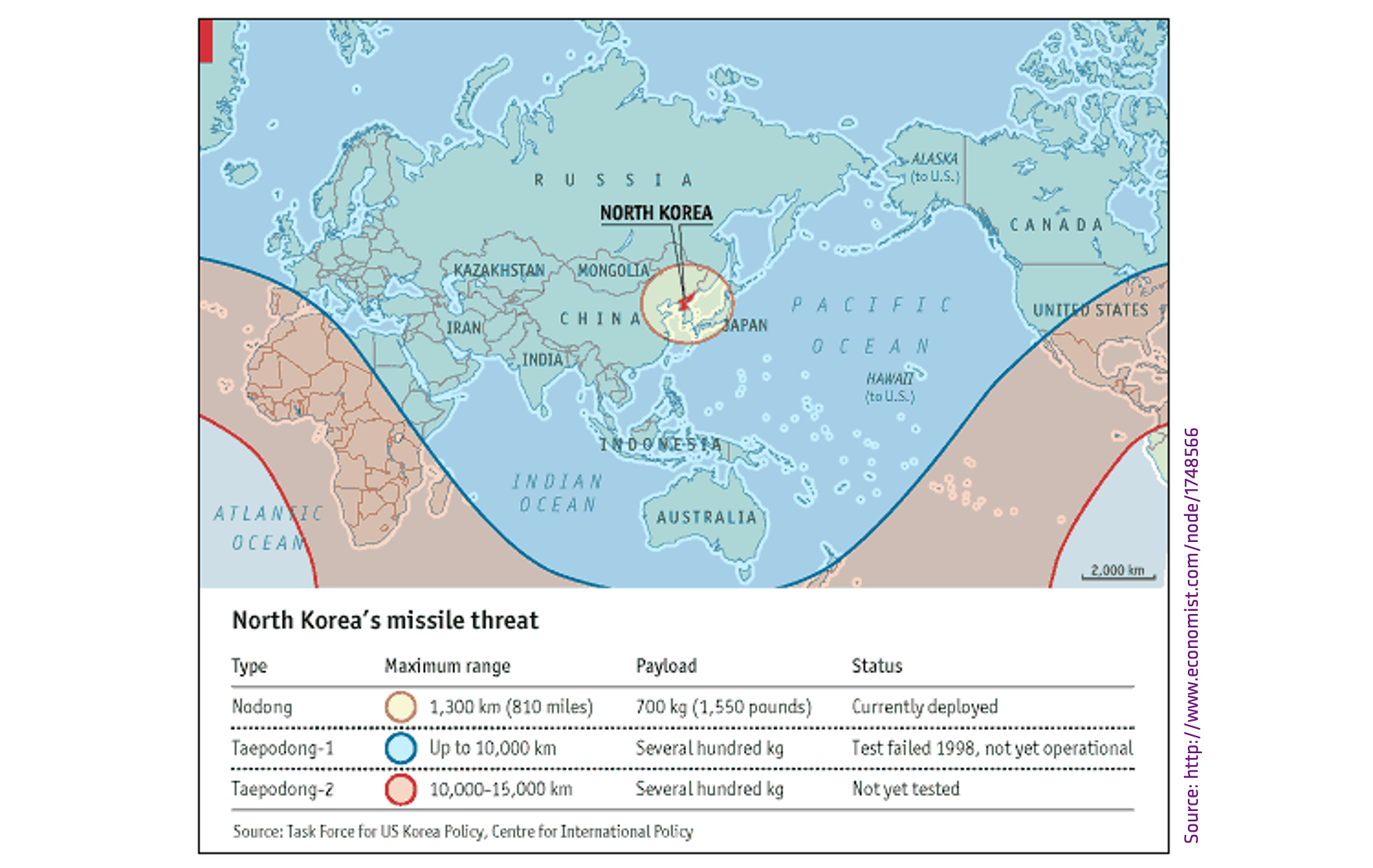
That’s Better!

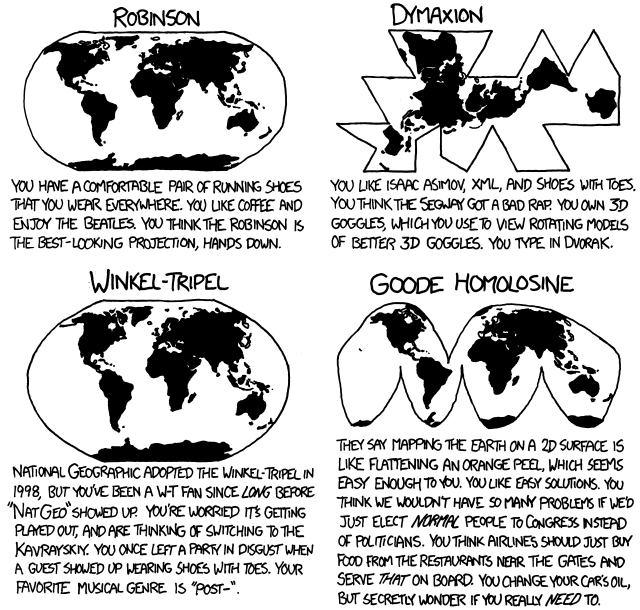
What’s a Projection?

Source

Are spatial (a.k.a. geometrical) transformations any different from the other mathematical transformations covered in this session?

Data exists in a ‘space’ that we can transform and manipulate in various ways using functions to serve our exploratory and analytical purposes.

Resources

Transformation • Jon Reades