Grouping Data

Jon Reades

Useful, But Limited?

Method	Achieves
count()	Total number of items
first(), last()	First and last item
mean(), median()	Mean and median
min(), max()	Minimum and maximum
std(), var()	Standard deviation and variance
mad()	Mean absolute deviation
prod()	Product of all items
sum()	Sum of all items

Here are a bunch of pandas functions that have to do with aggregating data in some way. Some of these you’ll have seen before, some you may not. However, up to this point if you wanted to to know the median price of each type of Airbnb listing, or the sum of each type of vehicle sold, you’d have had to select out one listing type or vehicle type, call median or sum, and then remember the result. Let’s change that.

Grouping Operations

In Pandas these follow a split / apply / combine approach:

Note that, for simplicity, I’ve abbreviate the Local Authority names since this is just a simplified example: TH (Tower Hamlets), HAK (Hackney), W (Westminster).

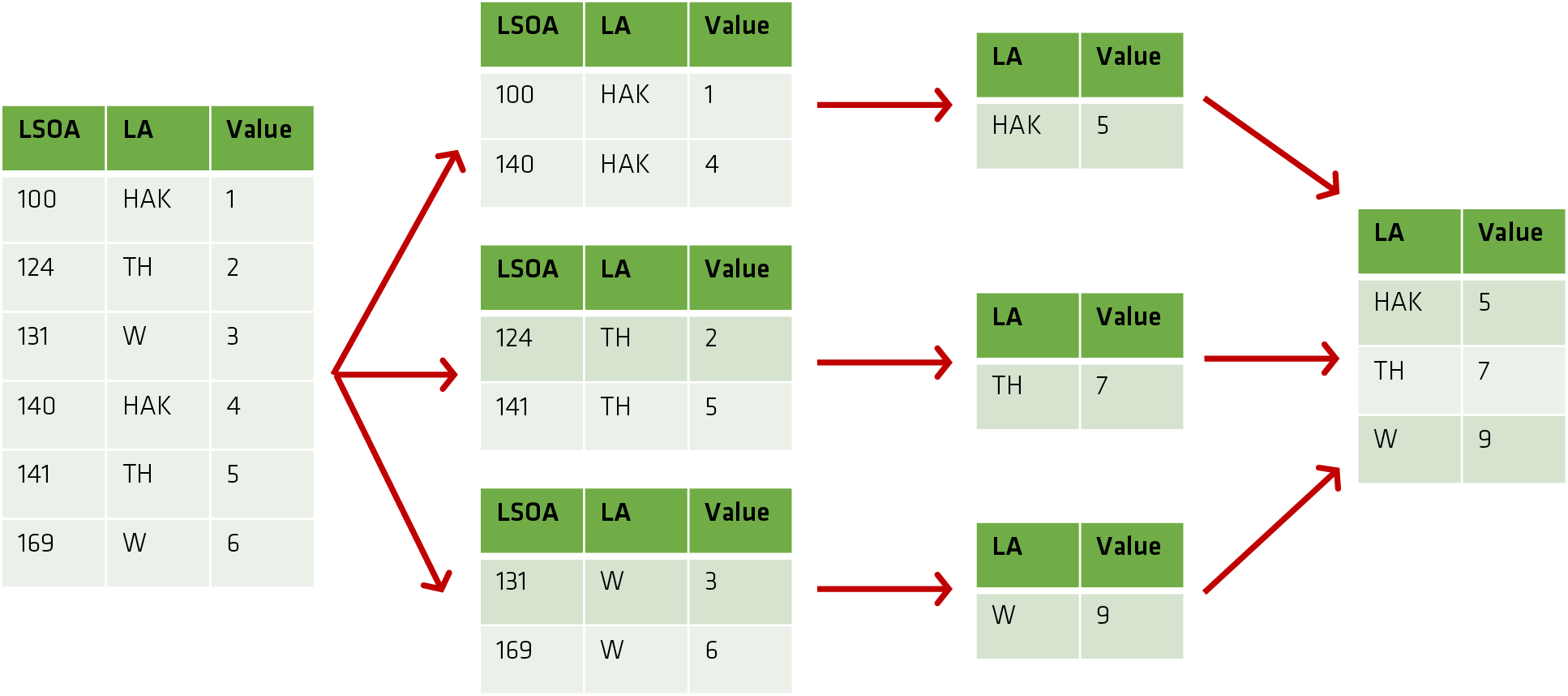
In Practice

grouped_df = df.groupby(<fields>).<function>

For instance, if we had a Local Authority (LA) field:

grouped_df = df.groupby('LA').sum()

Using apply the function could be anything:

def norm_by_data(x): # x is a column from the grouped df
    x['d1'] /= x['d2'].sum() 
    return x

df.groupby('LA').apply(norm_by_data)

Grouping by Arbitrary Mappings

mapping = {'HAK':'Inner', 'TH':'Outer', 'W':'Inner'}
df.set_index('LA', inplace=True)
df.groupby(mapping).sum()

Pivot Tables

A ‘special case’ of Group By features:

• Commonly-used in business to summarise data for reporting.
• Grouping (summarisation) happens along both axes (Group By operates only on one).
• pandas.cut(<series>, <bins>) can be a useful feature here since it chops a continuous feature into bins suitable for grouping.

In Practice

age = pd.cut(titanic['age'], [0, 18, 80])
titanic.pivot_table('survived', ['sex', age], 'class')

Deriving Measures of Diversity

One of the benefits of grouping is that it enables us to derive measures of density and diversity; here are just a few… Location Quotient (LQ), Herfindah-Hirschman Index (HHI), Shanon Entropy.

I like easy measures.

Location Quotient

The LQ for industry i in zone z is the share of employment for i in z divided by the share of employment of i in the entire region R. \[ LQ_{zi} = \dfrac{Emp_{zi}/Emp_{z}}{Emp_{Ri}/Emp_{R}} \]

	High Local Share	Low Local Share
High Regional Share	\[\approx 1\]	\[< 1\]
Low Regional Share	\[> 1\]	\[\approx 1\]

In other words, this is a type of standardisation that enables to compare the concentration of Investment Bankers with the concentration of Accountants, even if there are many more Accountants than Bankers! But this can also apply to the share of flats to whole-property lettings just as easily.

Note that this is influenced by small sample sizes (e.g. the number of Fijians in Britain).

Herfindahl-Hirschman index

The HHI for an industry i is the sum of squared market shares for each company in that industry: \[ H = \sum_{i=1}^{N} s_{i}^{2} \]

Concentration Level	HHI
Monopolistic: one firm accounts for 100% of the market	\[1.0\]
Oligopolistic: top five firms account for 60% of the market	\[\approx 0.8\]
Competitive: anything else?	\[< 0.5\]?

If \(s_{i} = 1\) then \(s_{i}^{2} = 1\), while if \(s_{i} = 0.5\) then \(s_{i}^{2} = 0.25\) and \(s_{i} = 0.1\) then \(s_{i}^{2} = 0.01\).

This can be translated to compare, for instance, local and regional neighbourhood diversity: some cities are ethnically diverse in aggregate but highly segregated at the local level.

Note that this is influenced by the number of ‘firms’ (or ethnicities or…).

Shannon Entropy

Shannon Entropy is an information-theoretic measure: \[ H(X) = - \sum_{i=1}^{n} P(x_{i}) log P(x_{i}) \]

I often think of this as ‘surprise’: a high entropy measure means that it’s hard to predict what will happen next. So randomness has high entropy. By extension, high concentration has low entropy (even if the result is surprising on the level of intuition: I wasn’t expecting to see that) because I can predict a 6 on the next roll of the dice fairly easy if all of my previous rolls were 6s.

Resources

• Stop aggregating away the signal in your data