Clustering

Jon Reades - j.reades@ucl.ac.uk

1st October 2026

Spot the Difference

Classification

• Allocates n samples to k groups
• Works for different values of k
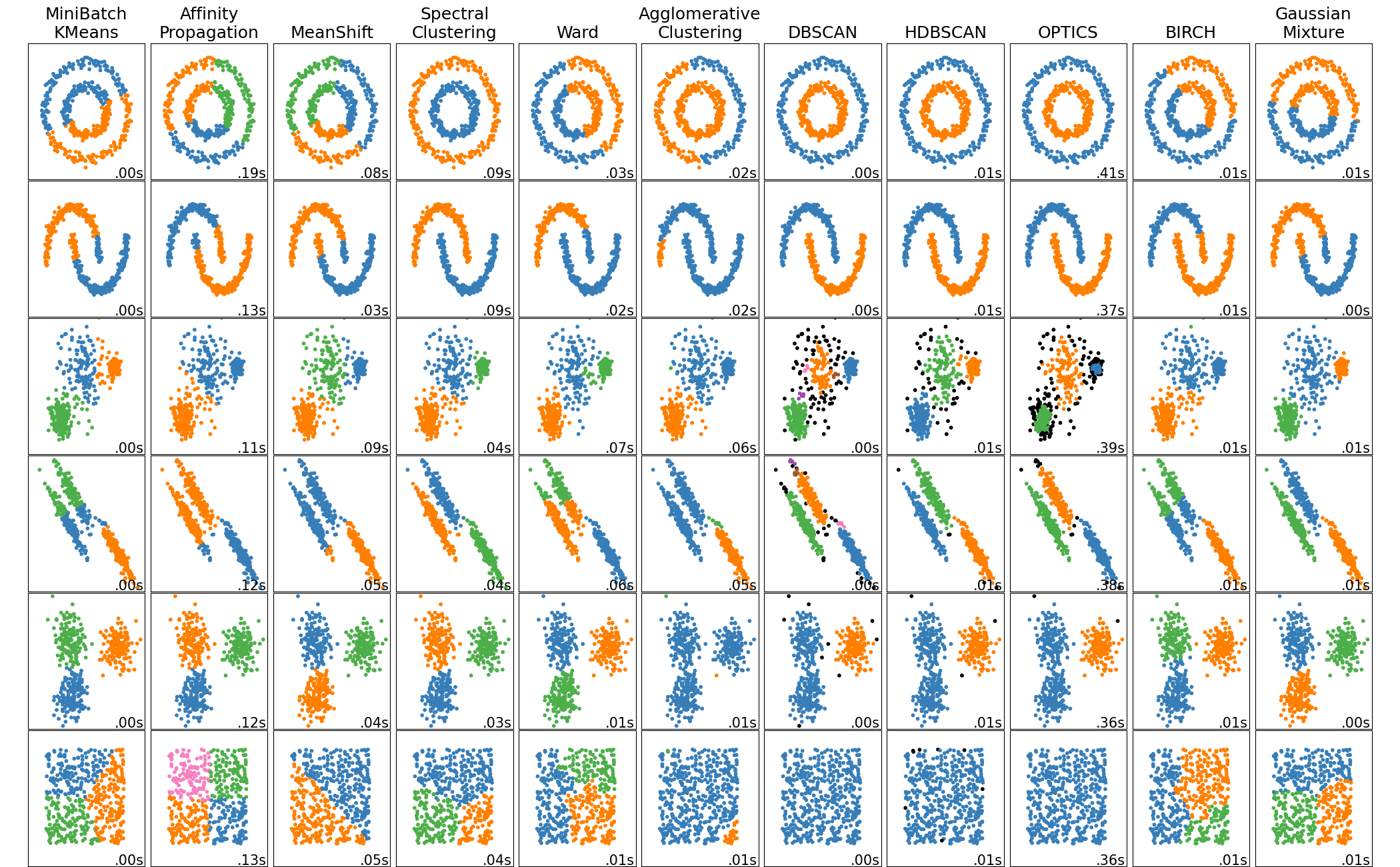
• Different algorithms (A) present different views of group relationships
• Poor choices of A and k lead to weak understanding of data
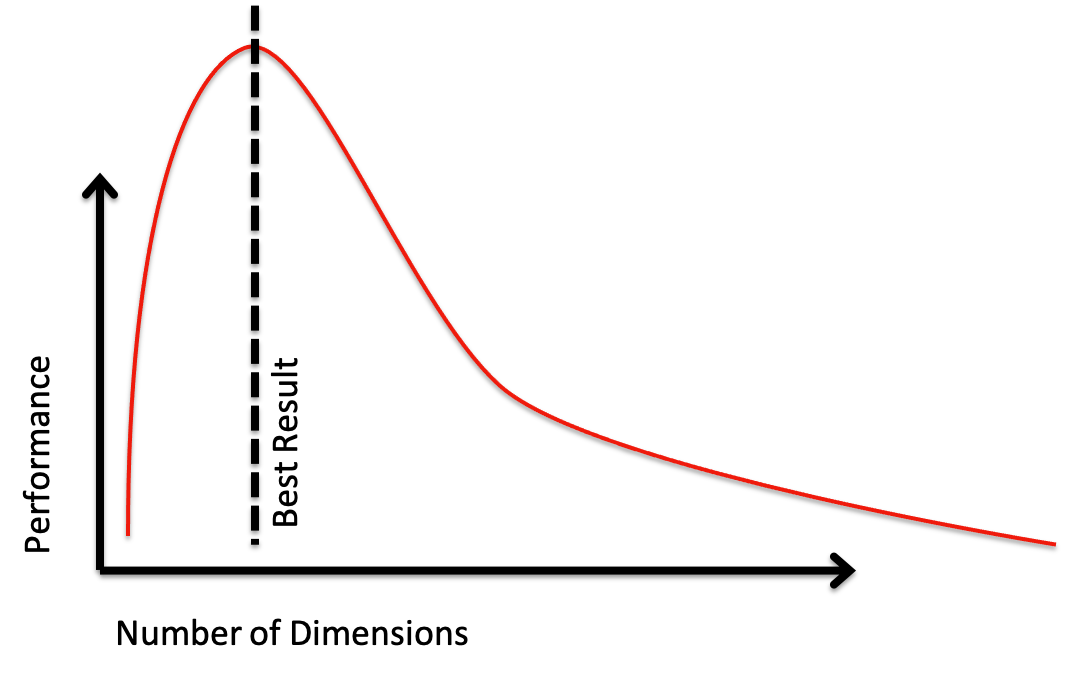
• Typically works best in 1–2 dimensions

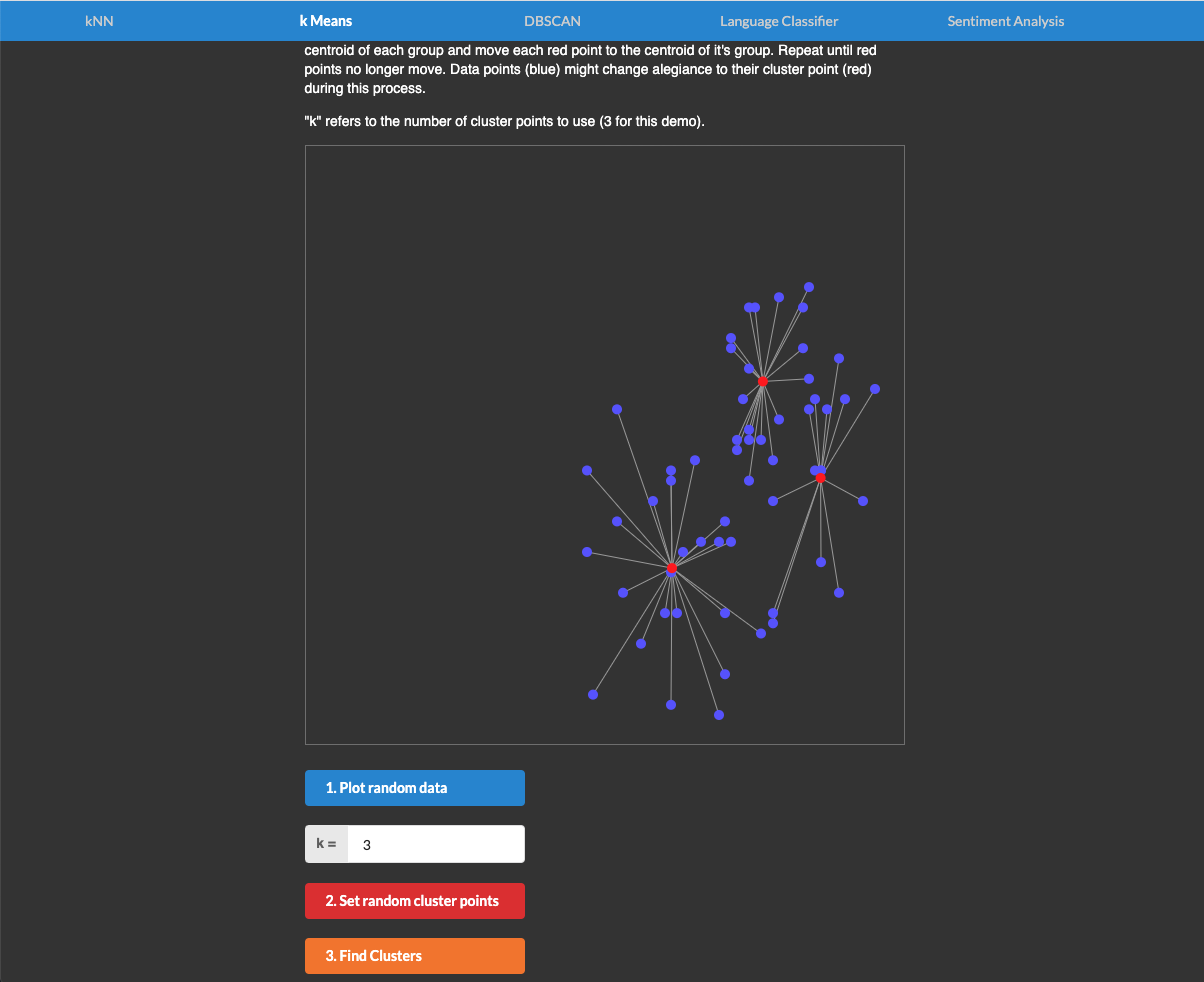
Clustering

• Allocates n samples to k groups
• Works for different values of k
• Different algorithms A present different views of group relationships
• Poor choices of A and k lead to weak understanding of data
• Typically works best in < 9 dimensions

Clustering algorithms can suffer from the ‘curse of dimensionality’ such that high-dimensional spaces cluster poorly without either dimensionality reduction or the use of specialist algorithms such as Spherical k-Means.

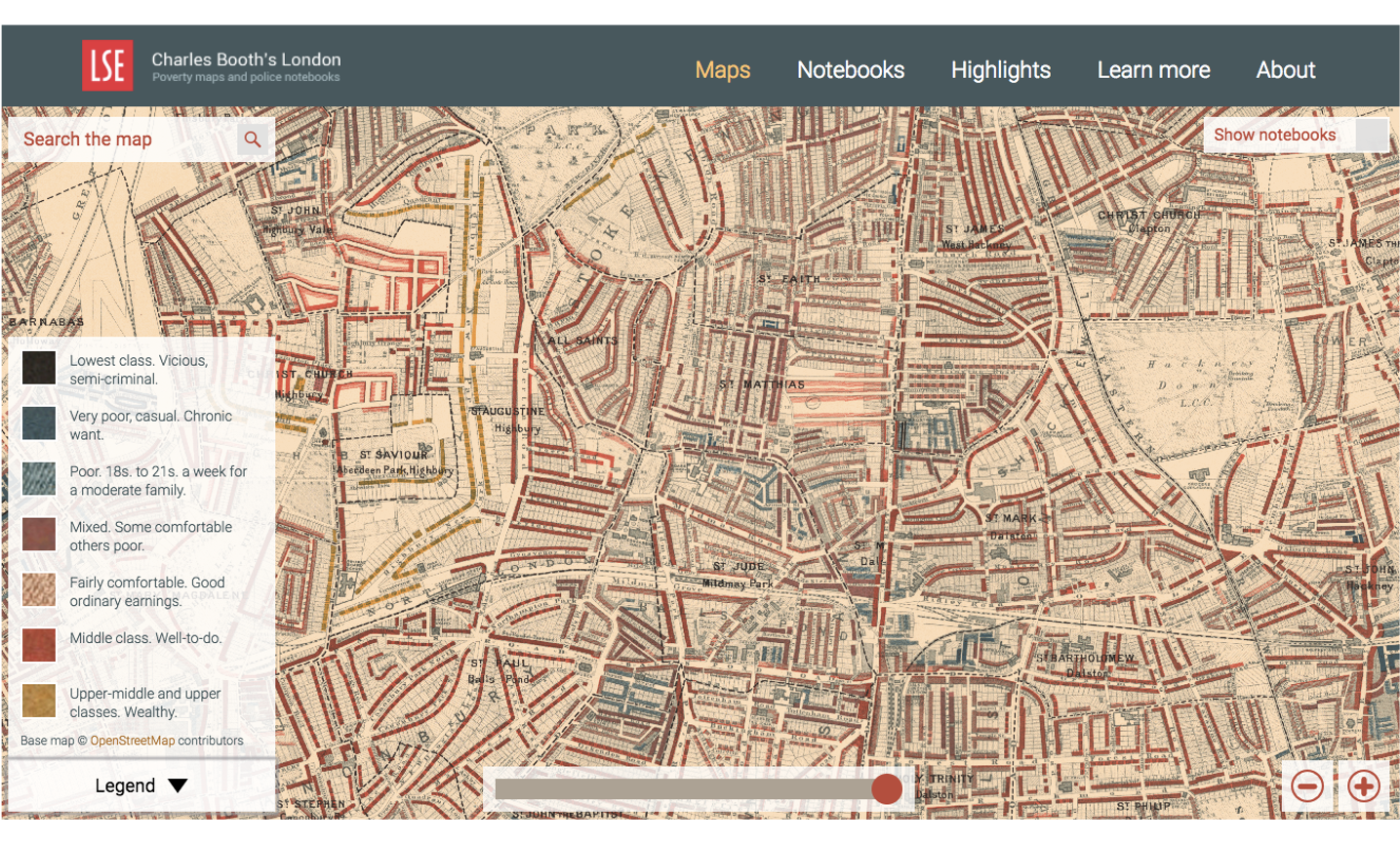
The First Geodemographic Classification?

Source: booth.lse.ac.uk/map/

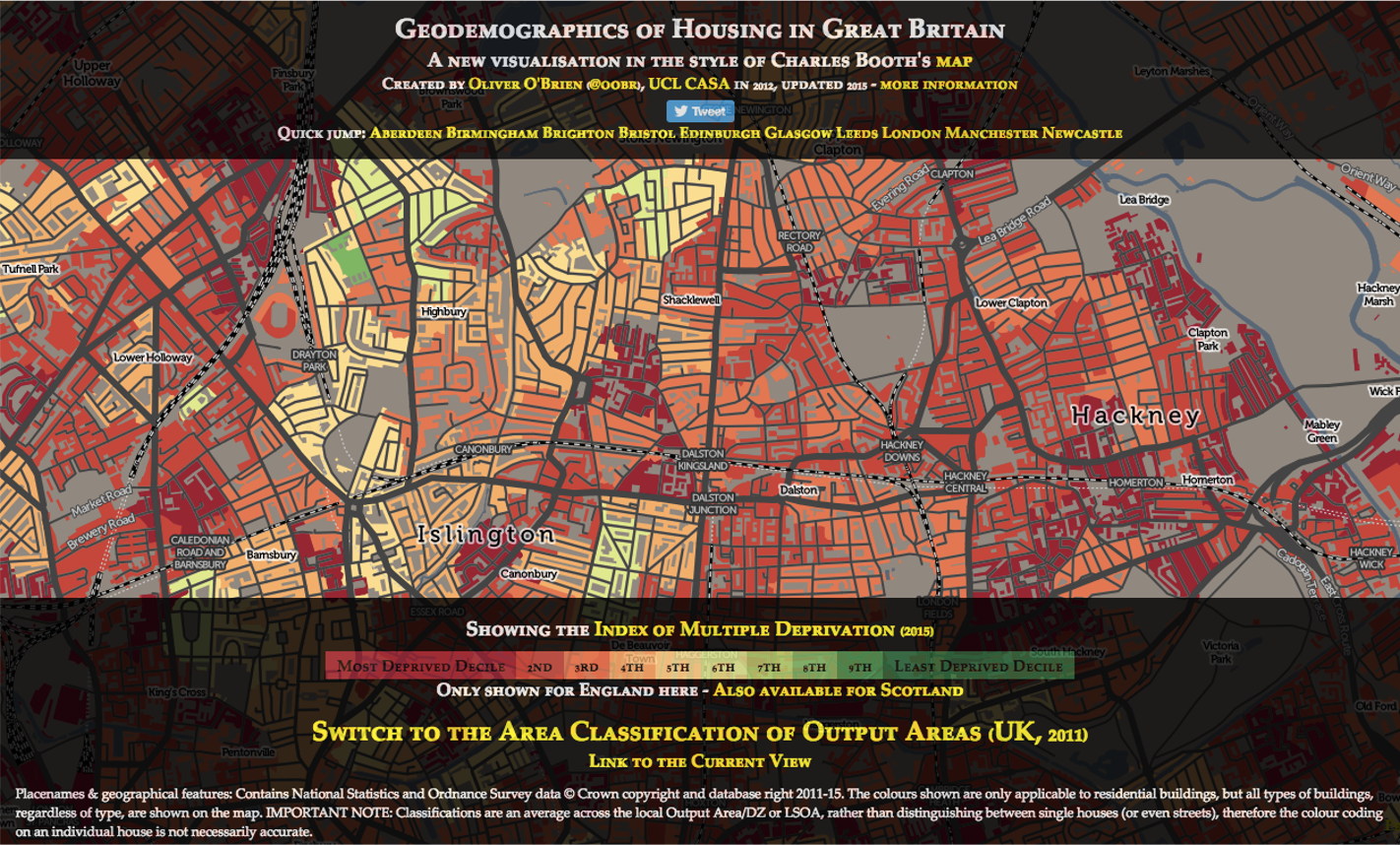
More than 100 Years Later

Source: vis.oobrien.com/booth/

Intimately Linked to Rise of The State

• Geodemographics only possible in context of a State – without a Census it simply wouldn’t work… until now?
• Clearly tied to social and economic ‘control’ and intervention: regeneration, poverty & exclusion, crime, etc.
• Presumes that areas are the relevant unit of analysis; in geodemographics these are usually called neighbourhoods… which should ring a few bells.
• In practice, we are in the realm of ‘homophily’, a.k.a. Tobler’s First Law of Geography

Where is it used?

Anything involving grouping individuals, households, or areas into larger ‘groups’…

• Strategic marketing (above the line, targeted, etc.)
• Retail analysis (store location, demand modelling, etc.)
• Public sector planning (resource allocation, service development, etc.)

Could see it as a subset of customer segmentation.

Computational Context

Problem Domains

	Continuous	Categorical
Supervised	Regression	Classification
Unsupervised	Dimensionality Reduction	Clustering

• In classification we ‘know’ the answer (we test against labels).
• In clustering we don’t ‘know’ the answer (we look for clusters).

> What is a cluster?

A group of similar data points.

> What is the purpose of clustering?

To generalise from ‘raw’ data.

Measuring ‘Fit’

Usually working towards an ‘objective criterion’ for quality… these are known as cohesion and separation measures.

How Your Data Looks…

Clustering is one area where standardisation (and, frequently, normalisation) are essential:

• You don’t (normally) want scale in any one dimension to matter more than scale in another.
• You don’t want differences between values in one dimension to matter more than differences in another.
• You don’t want skew in one dimension to matter more than skew in another.

You also want uncorrelated variables… why?

First Steps

You will normally want a continuous variable… so these types of data are especially problematic:

• Dummies / One-Hot Encoded
• Categorical / Ordinal
• Possible solutions: k-modes, CCA, etc.

Performance

Typically about trade-offs between:

• Accuracy
• Generalisation

Trade-Offs

Need to balance:

• Ability to cluster at speed.
• Ability to replicate results.
• Ability to cope with fuzzy/indeterminate boundaries.
• Ability to cope with curse of dimensionality.
• Underlying representation of group membership…

Visualising the Trade-Offs

Notice the limitations to k-means: it may be fast but it’s got problems if your data is non-linear/non-Gaussian.

And this doesn’t even include options like HDBSCAN, HAC/Hierarchical Clustering, and many more!

Details on scikit-learn.org.

Interactive Demo.

Putting it All into Context