Randomness

Jon Reades - j.reades@ucl.ac.uk

1st October 2025

Many things are surprisingly non-random…

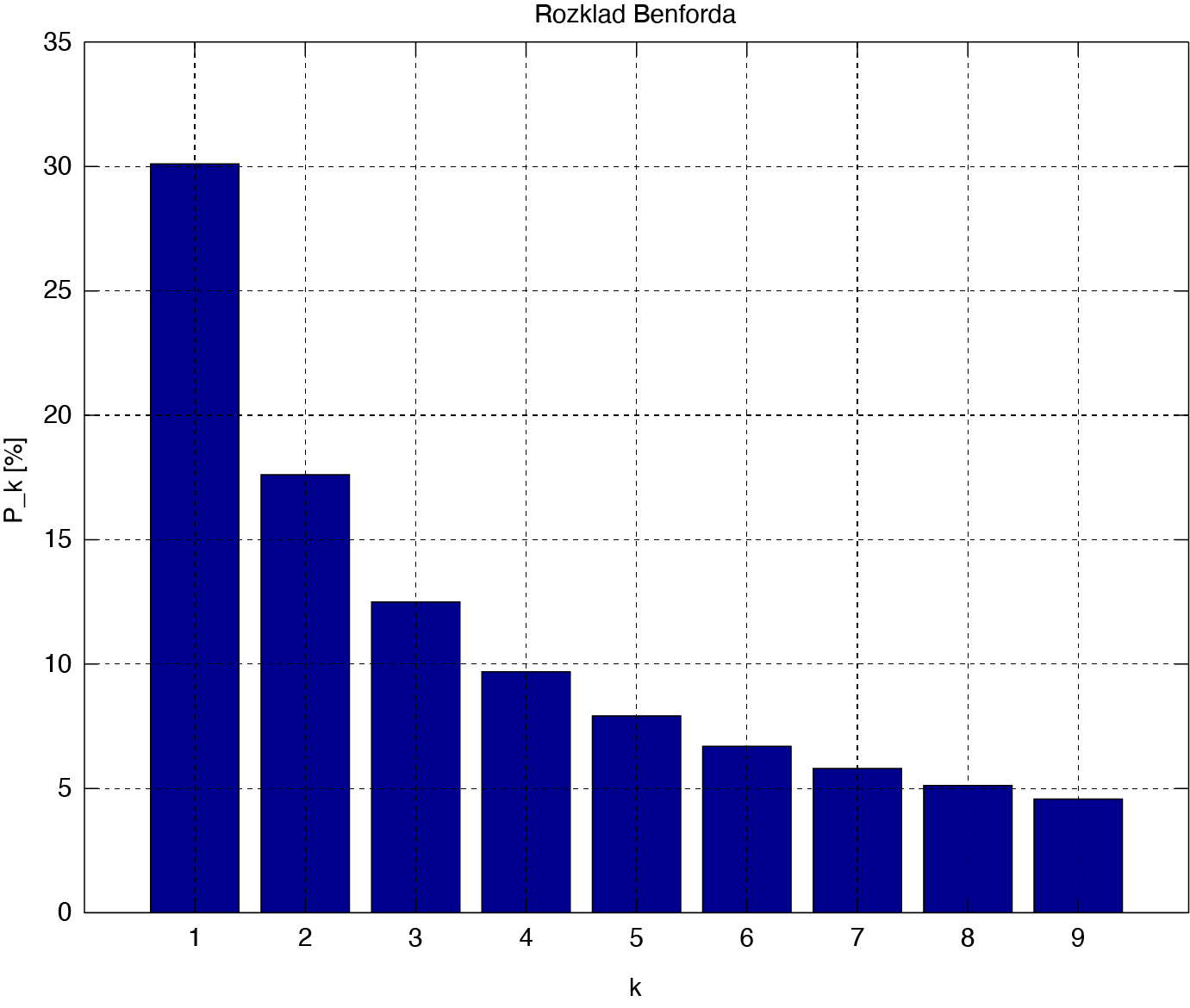
Benford’s Law, which has applications in data science and fraud detection.

Genuine randomness is hard. Most of us, both humans and computers, tend to use shortcuts when generating random numbers.

People are really bad at generating random numbers. Bendford’s law is used by auditors to look for abnormalities in financial returns.

Computers are better, but they are also lazy.

Reproducibility: Good or Bad?

Depends on the problem:

• Banking and encryption?
• Sampling and testing?
• Reproducing research/documentation?

OK, technically, even encryption needs to be reproducible to allow for decryption, but you sure don’t want it to be easy.

Not Very Good Encryption

Cyphertext	Output
ROT0	To be or not to be, That is the question
ROT1	Up cf ps opu up cf, Uibu jt uif rvftujpo
ROT2	Vq dg qt pqv vq dg, Vjcv ku vjg swguvkqp
…	…
ROT9	Cx kn xa wxc cx kn, Cqjc rb cqn zdnbcrxw

ROT is known as the Caesar Cypher, but since the transformation is simple (A..Z+=x) decryption is easy now. How can we make this harder?

Python is Random

import random
for i in range(0,10):
    print(random.randint(0,10))

1
9
6
0
0
1
3
3
8
9

See also: random.randrange, random.choice, random.sample, random.random, random.gauss, etc.

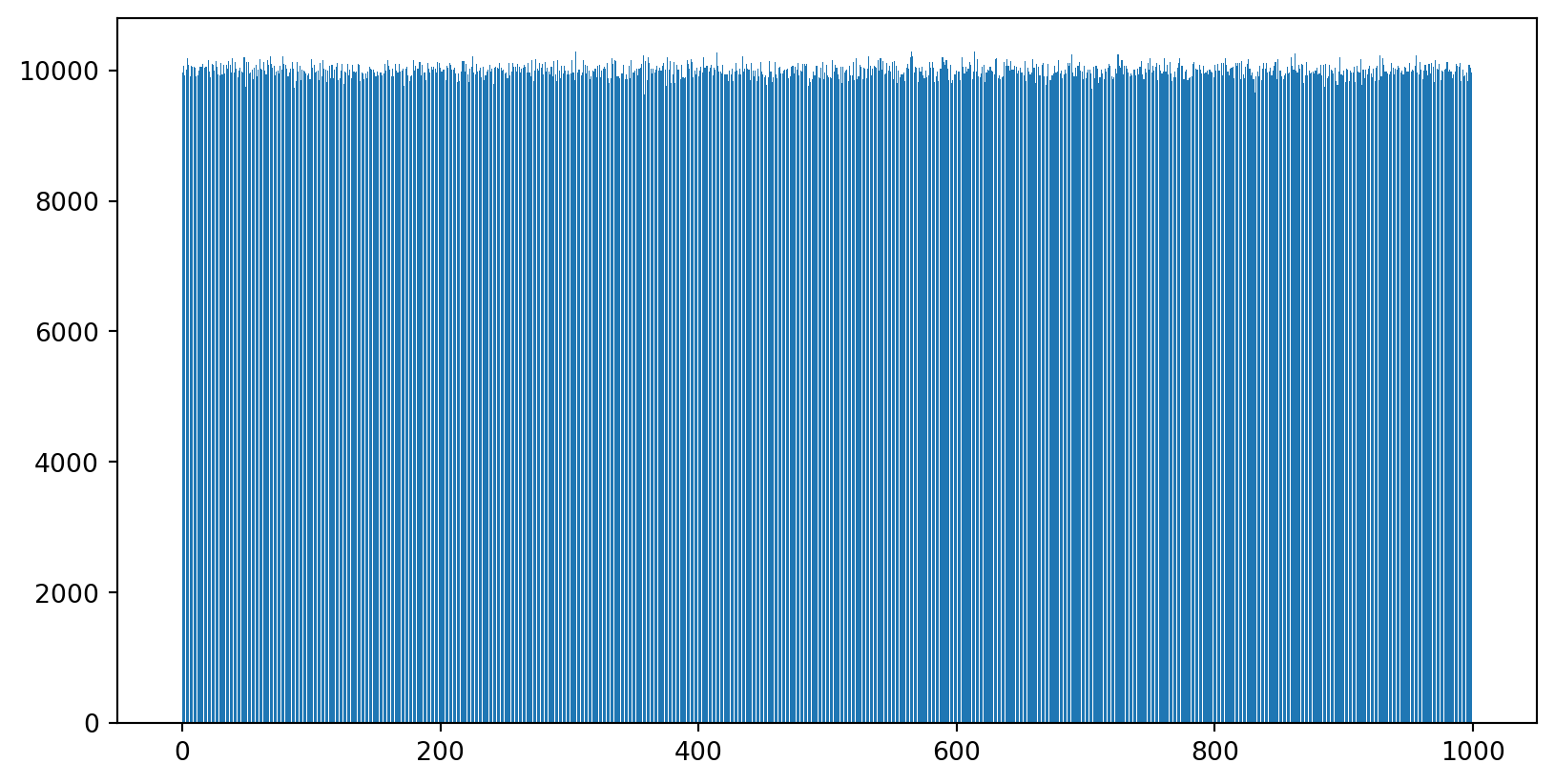
And Repeat…

import random
size = 10
results = [0] * size

tests = 100000
while tests > 0:
    results[random.randint(0,len(results)-1)] += 1
    tests -= 1

for i in range(0,len(results)):
    print(f"{i} -> {results[i]}")

0 -> 9995
1 -> 10100
2 -> 10099
3 -> 9865
4 -> 9908
5 -> 9874
6 -> 10121
7 -> 10110
8 -> 9859
9 -> 10069

What will this return?

Will it hold for more than 10 numbers?

Aaaaaaaaaaand Repeat

import random 
from matplotlib import pyplot as plt
import numpy as np

size = 1000
data = [0] * size

tests = 10000000
while tests > 0:
    data[random.randint(0,len(data)-1)] += 1
    tests -= 1

Answer on next slide…

Aaaaaaaaaaand Repeat

fig = plt.figure()
plt.bar(np.arange(0,len(data)), data)

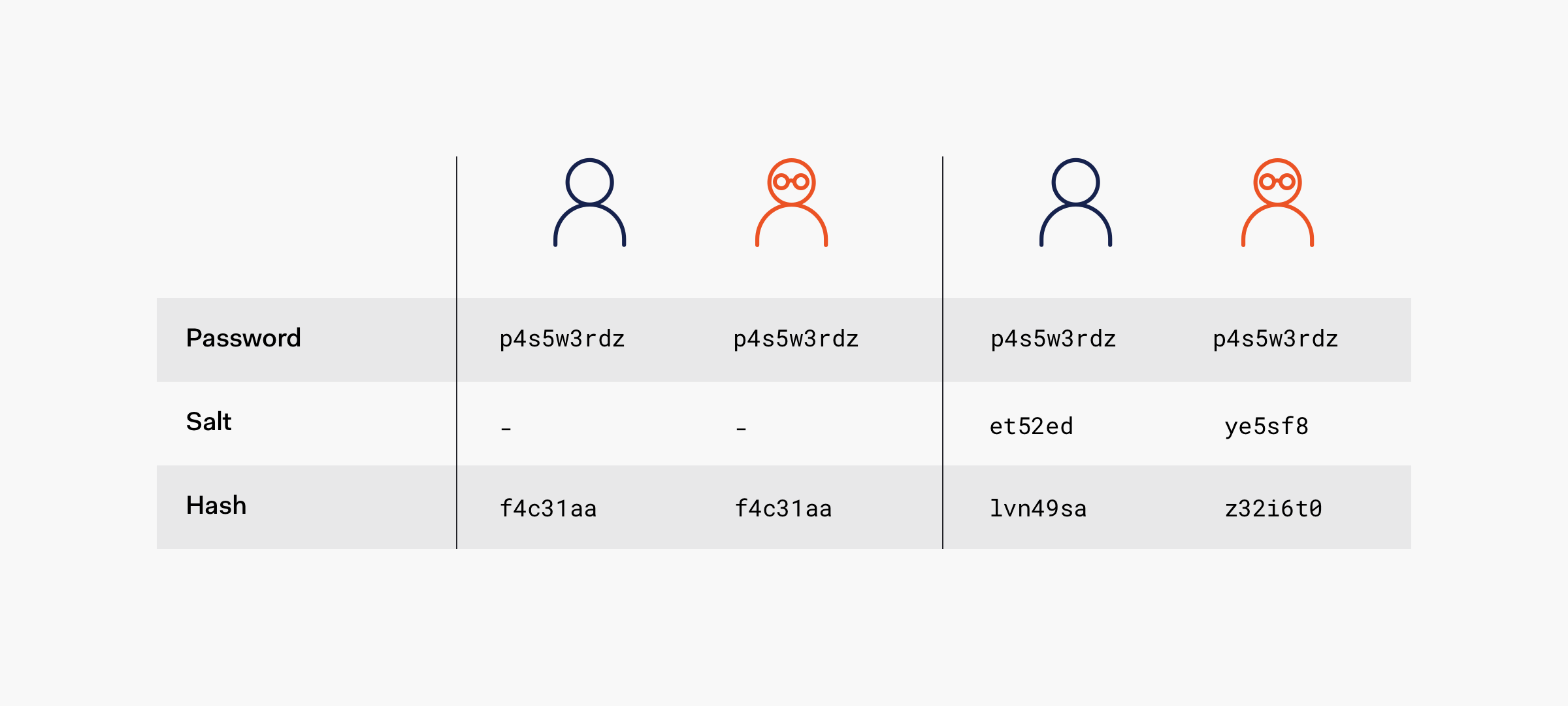
Seeds and Salts

Computers are pseudo-random number generators. Seeds and salts ensure different outputs from the same inputs.¹

How does that work? Well when you are hashing data a salt combines with the input to generate an ouput that is one-way only — if you use different salts for different users then an attacker who gains access to your account’s salt still needs to guess lots of passwords to see which one combines with the salt to generate your passward hash. But encryption is reversible, so if I know how you generated the output then I can reverse it to get the input — an encrypted message.

• Hashing is irreversible therefore cannot be compressed and is not a form of encryption as it is a one-way function
• Salt is added before hashing → then hashed
• Salts are different even if the seed is the same
• Digest is the result of hashing → a unique format
• Digests are the same if the seed is the same
• Encryption is reversible with a decryption key, while hashing is one-way and irreversible
• Digests and Salts are not forms of Encryption

1. I like schroeder’s Stack Exchange explanation of the difference.

Just add salt

Hashing

Spot the difference:

import hashlib # Can take a 'salt' (similar to a 'seed')

r1 = hashlib.md5('CASA Intro to Programming'.encode())
print(f"The hashed equivalent of r1 is: {r1.hexdigest()}")

r2 = hashlib.md5('CASA Intro to Programming '.encode())
print(f"The hashed equivalent of r2 is: {r2.hexdigest()}")

r3 = hashlib.md5('CASA Intro to Programming'.encode())
print(f"The hashed equivalent of r3 is: {r3.hexdigest()}")

The hashed equivalent of r1 is: acd601db5552408851070043947683ef
The hashed equivalent of r2 is: 4458e89e9eb806f1ac60acfdf45d85b6
The hashed equivalent of r3 is: acd601db5552408851070043947683ef

This is like generating a ‘fingerprint’ of an application or file. In fact, it’s what is going on behind the scenes when you download something to install on macOS or Windows and you’re told that the installer is being ‘verified’ before it will run: the computer is generating a hash of the application’s codebase, and sending that to the Apple Store or Windows Store or direct to the developer in order to check that the file hasn’t been tampered with.

And Note…

import requests
night = requests.get("http://www.gutenberg.org/ebooks/1514.txt.utf-8")
print(f"The text is '{night.text[32:63].strip()}'")
print(f"The text is {len(night.text):,} characters long")
hash = hashlib.md5(night.text.encode())
print(f"This can be hashed into: {hash.hexdigest()}")

The text is 'A Midsummer Night's Dream'
The text is 119,968 characters long
This can be hashed into: 2bd4cfe946d9a97d9ed07631450196af

Can be applied to anything: even one byte’s difference (e.g. in a application) can lead to a different hash output.

But notice that hashes are always the same length. This property is quite useful for databases and verifying the integrity of applications (MD5 Checksums).

JupyterLab Password

To set a password in JupyterLab you need something like this:

sha1:d36ae21ea7f84801:2f60d6dba76a2b51ba884eb591cdb36e9f8f4dd2

How this was generated:

import uuid, hashlib
salt = uuid.uuid4().hex[:16] # Truncate salt
password = 'casa2021'        # Set password

# Here we combine the password and salt to 
# 'add complexity' to the hash
hashed_password = hashlib.sha1(password.encode() + 
                  salt.encode()).hexdigest()
print(':'.join(['sha1',salt,hashed_password]))

sha1:4b75f2c47bdb41b1:2aa2a7ad58cfc4204fae2d8c029a629df18f1513

Then you can replace the JUPYTER_PWD parameter in the start-up string for Podman/Docker if you want to set a password.

Note: don’t set your passwords this way.

Encryption & Security

Simple hashing algorithms are not normally secure enough for operational use. Genuine security training takes a whole degree + years of experience.

Areas to look at for more secure computing:

• Public and Private Key Encryption (esp. OpenSSL)
• Privileges used by Applications (esp. Podman vs Docker)
• Revocable Tokens (e.g. for APIs)
• Injection Attacks (esp. for SQL using NULL-byte and similar)

Back to Randomness

Two main libraries where seeds are set:

import random
random.seed(42)

import numpy as np
np.random.seed(42)

Turning now from the security aspects, let’s look at other types seeds.

Why do you often see 42 used as a seed?

Seeds and State

import random
random.seed(42)
st = random.getstate()
for r in range(0,3):
    random.setstate(st)
    print(f"Repetition {r}:")
    ints = []
    for i in range(0,10):
        ints.append(random.randint(0,10))
    print(f"\t{ints}")

Repetition 0:
    [10, 1, 0, 4, 3, 3, 2, 1, 10, 8]
Repetition 1:
    [10, 1, 0, 4, 3, 3, 2, 1, 10, 8]
Repetition 2:
    [10, 1, 0, 4, 3, 3, 2, 1, 10, 8]

Question!

Where would you use a mix of randomness and reproducbility as part of a data analysis process?

Hint: With a large data set it will often be useful to be able draw a random… what? But for reproducible analysis we will that random… what?… to be the same each time!

Thank You

References